Solution - Combinatorial Logic
Overview
Subtractor
Let A and B unsigned numbers encoded in N bits. Their binary representations are given by
\[ A = \sum_{i=0}^{n-1}A_{i}2^{i}, \quad B = \sum_{i=0}^{n-1}B_{i}2^{i}, \quad \text{where}\; A_i, B_i \in {0, 1} \]
Then their difference \(D = A-B\) is given by
\[ D= \sum_{i=0}^{n-1} (A_{i}-B_{i})2^{i} \]
In the above equation, the range of the individual weights is \(A_i-B_i \in \{-1, 0, 1\}\). So there are three different values, which we can encode in 2 bits \(\{C_{i+1},D_i\}\), where \(D_i\) is the (positive) difference bit, and \(C_{i+1}\) is the carry bit with negative weight. The result of the difference between the two bits is thus a 2-bit number encoded in 2's complement form.
The arithmetic equation connecting the inputs and outputs is therefore:
\[ A_i-B_i = -2 \cdot C_{i+1}+D_{i} \]
We need to generalise this equation in order to take into account en incoming carry bit. Having shown that the difference on two bits generates a carry with negative sign, we can conclude that the incoming carry will be of negative sign, too, resulting in the computation \(A_i - B-i - C_i\). The result has the range \(\{-2,-1,0,1\}\), which can again be represented as a 2-bit number encoded in 2's complement form.
As a conclusion, the complete equation for the subtractor is given by:
\[ A_i-B_i-C_i = -2\cdot C_{i+1}+D_i \]
Here is the truth table for the subtractor:
| \(A_i\) | \(B_i\) | \(C_{i}\) | \(A_i-B_i-C_i\) | \(C_{i+1}\) | \(D_i\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | -1 | 1 | 1 |
| 0 | 1 | 0 | -1 | 1 | 1 |
| 0 | 1 | 1 | -2 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | -1 | 1 | 1 |
Starting from the above table, after some simplifications, we obtain the Boolean equations:
\[ C_{i+1} = \overline{A_i} B_i + \overline{A_i}C_i + B_i C_i \]
\[ D_i = A_i \oplus B_i \oplus C_i \]
These equations can be implemented as a combinatorial circuit as follows:
Comparing the structure to the full adder circuit, we can see that the two circuits are almost identical, except for the two inverters at the AND gates for the carry calculation.
Adder-Subtractor
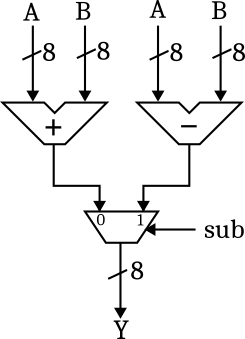
A first solution is to use separate circuits for addition and subtraction (for example using the above subtractor circuit in the same way as a carry-ripple adder) and selecting the appropriate result with a multiplexer.
Can we do better? The answer is yes: We can calculate the difference with the adder circuit by feeding \(-B\) into the second input, since \(A-B\) is just \(A+(-B)\). But how do we compute \(-B\)? Remember from the first lecture on combinatorial logic that for a number represented in two's complement
\[ -B = \overline{B} + 1 \]
So computing \(-B\) can be done by inverting each individual bit of \(B\) and adding 1. So does this mean that we need a second adder circuit to compute \(-B\)? In this case, we wouldn't have gained anything, and the propagation time of the circuit would be even worse than in the first solution. It turns out that we can use the following trick: Since we do not have an incoming carry bit, we can use the carry input of the adder circuit to add 1 in case of subtraction. On the input side, we need to select among \(B\) and \(\overline{B}\):
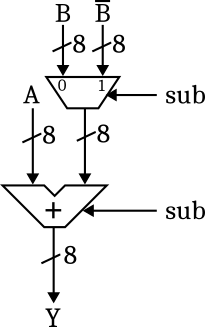
In the last step, we can slightly optimize the input part by observing that selecting \(B\) or \(\overline{B}\) is actually a controlled negation, which can be realised using exclusive or gates:
