Homework — Propagation Time
Overview
Carry-Ripple Adder
Consider the carry-ripple adder presented in the lecture:
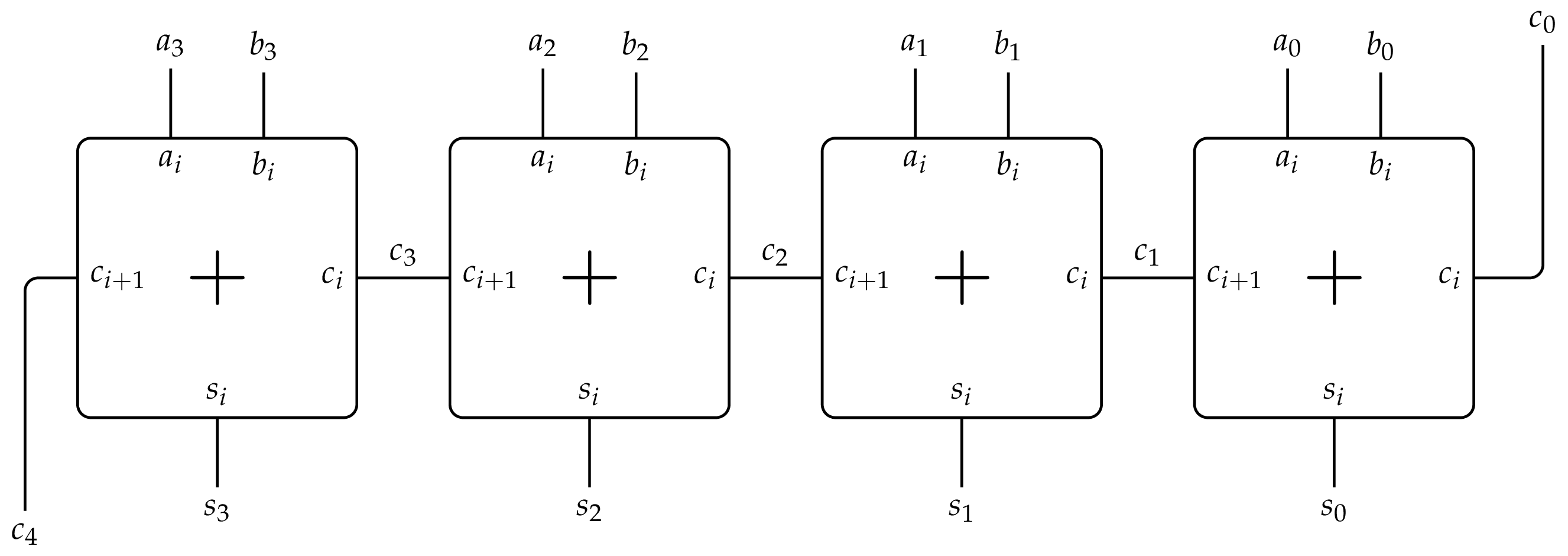
We would like to determine the computation time of this operator for inputs (and outputs) of size \(P\). We consider the following propagation times for a full adder cell:
- Propagation time from any input to the carry output: 1 ns
- Propagation time from any input to the sum output: 2 ns
Question 1: Find the computation time of the carry-ripple adder of size \(P\).
In the following, we would like to generalize this result to the addition of \(2^Q\) operands of \(P\) bits each.
Question 2: Propose a structural design of a combinatorial operator computing the sum of \(2^Q\) operands of \(P\) bits, using \(P\)-bit carry-ripple adders. In a first attempt, we will not consider overflows, all intermediate results and the final result shall be of size \(P\). The design shall have a minimal number of layers in order to minimize the computation time.
Question 3: Find the computation time of this operator depending on \(P\) and \(Q\).
Question 4: If we want the computation to be accurate, how many bits do we need at each layer of adders?
A Faster Addition
The principal problem with the carry-ripple adder is the length of its critical path (the carry chain). There are several alternative structures which have lower propagation time, but which need more logic gates. One of such designs – called carry-select adder – is shown in the figure below. It implements an 8-bit adder using several 4-bit (carry-ripple) adders and some multiplexers:
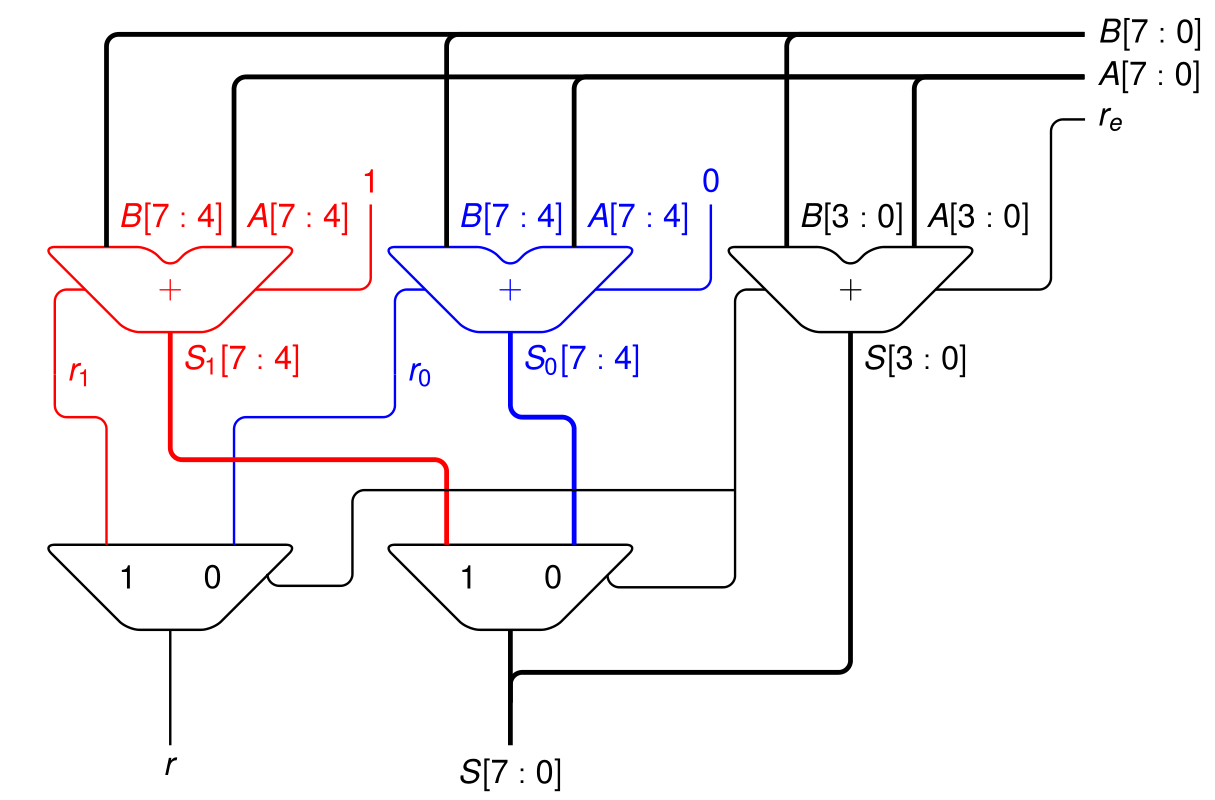
Question 1: Explain how the design works.
We consider the following propagation times for basic elements (full adder, multiplexer):
- Propagation time from any input to the carry output: 1 ns
- Propagation time from any input to the sum output: 2 ns
- Propagation time of a multiplexer: 1 ns
Question 2: With the above information, establish the computation time of the carry-select adder.
Question 3: Compare the result with the carry-ripple adder.
The Maximum Operator (Again)
This exercise is the continuation of the corresponding exercise in TD Combinatorial Logic.
We consider the following propagation times:
- For the subtractor (1-bit), from any input to any output: 1 ns
- For the multiplexer: 1 ns
- For the elementary 1-bit maximum operator (design in question 5), from any input to any output: 1 ns
Question 1: Using the arithmetic solution you proposed in question 1, compute the propagation time needed to find the maximum between 4 numbers (use a tree structure).
Question 2: Using the solution you proposed in question 5, compute the propagation time needed to find the maximum between 4 numbers (use a tree structure).
Question 3: Compare the two solutions and extrapolate for \(2^Q\) numbers.